Destruction of the World Trade Center North Tower and Fundamental Physics

Abstract: The roof line of the North Tower of the World Trade Center is shown to have been in constant downward acceleration until it disappeared. A downward acceleration of the falling upper block implies a downward net force, which requires that the upward resistive force was less than the weight of the block. Therefore the downward force exerted by the falling block must also have been less than its weight. Since the lower section of the building was designed to support several times the weight of the upper block, the reduced force exerted by the falling block was insufficient to crush the lower section of the building. Therefore the falling block could not have acted as a “pile driver.” The downward acceleration of the upper block can be understood as a consequence of, not the cause of, the disintegration of the lower section of the building.

Introduction

The destruction of the World Trade Center on September 11, 2001 was, by any assessment, a momentous turning point in world affairs. More than eight years after the event, the causes of the collapses of the three largest World Trade Center buildings (WTC 1, WTC 2, and WTC 7) remain hotly contested despite official reports by government agencies, first by FEMA then by NIST, attempting to lay the matter to rest. A “9/11 Truth Movement” has arisen, including over 1000 architects and engineers who are calling for a new investigation. The NIST investigators constructed an elaborate computer model of the buildings which they used to model the airplane crashes, but strangely they did not model the actual collapses of the Twin Towers. They took their analysis only up to the point of initiation of collapse, relying, as we shall see, upon a much more simplistic model proposed by Zdenĕk Bazănt[4, 5, 6, 7], which concluded that once the collapse was initiated, total collapse was inevitable.

What follows here is an analysis that follows the simplifying assumptions laid out by Bazănt. Using measurements and a level of analysis accessible to an introductory physics class, undergraduate students have it within their power to evaluate the adequacy of the NIST-Bazănt model. Their physics background, even at this stage, equips them for intelligent participation in a significant civic debate.

The Pile Driver

The twin towers of the World Trade Center were destroyed in a top-down manner. More particularly, the section of the building from about the 98^th floor upward to the roofline appeared to decouple and accelerate downward through the lower 98 floors. The mechanism of this process has been debated

both among those limiting their search to a strictly natural explanation of the catastrophe (plane impacts, fire, and gravity) and among those willing to evaluate all possible explanations (including pre- planted explosives). The destruction of a building is a complex process, but simple physics applied to the observed motion of the roofline can constrain the choices among proposed theories. We will focus here on the details of the destruction of the North Tower. It was the first building to be hit by a plane and the second building to fall on September 11, 2001. It can be identified as the tower with the large antenna on its roof. The theory published by Thomas W. Eagar and Christopher Musso in JOM in December 2001,[1] and adopted by the Federal Emergency Management Agency (FEMA) study, postulated that the floor connections broke due to fire, leading to a “pancaking” collapse of the floors. This theory does not provide an explanation for why the core structure also failed, and it was rejected by the National Institute of Standards and Technology (NIST) study. Instead, the NIST report focuses on column failure. On the FAQ page of NIST’s website we read:

NIST’s findings do not support the “pancake theory” of collapse, which is premised on a progressive failure of the floor systems in the WTC towers. (The composite floor system, that connected the core columns and the perimeter columns, consisted of a crossed grid of steel trusses integrated with a concrete slab.) Instead, the NIST investigation concluded that the collapse was caused by sagging floor trusses pulling on the south wall perimeter columns causing them to bow inward and eventually fail.

This mechanism requires that the floor trusses remain attached to the perimeter columns, so pancaking is ruled out.[2]

In NIST’s view, fire caused a critical number of core and perimeter columns to weaken and eventually fail near the impact zone. The following is from p. 151 of their summary document, NIST NCSTAR 1.

Collapse Initiation

• The bowed south wall columns buckled and were unable to carry the gravity loads.
  
  Those loads shifted to the adjacent columns via the spandrels, but those columns quickly became overloaded as well. In rapid sequence, this instability spread all the way to the east and west walls.
• The section of the building above the impact zone (near the 98th floor), acting as a rigid block, tilted at least 8 degrees to the south.
• The downward movement of this structural block was more than the damaged structure could resist, and global collapse began. [3]

A series of papers by Zdenĕk Bazănt,[4, 5, 6, 7] with various co-authors, describe what has become known as the “pile-driver” hypothesis, which appears to have been relied upon by the NIST investigation. Bazănt describes a scenario in which the top assembly of the building remains rigid as it crushes the lower sections of the building into rubble. Only when the lower section has been crushed into a compact debris pile does the top assembly crush itself. This proposed process has become known as “Crush-Down” followed by “Crush-Up.” His claim is that once collapse is initiated, it becomes inevitable. Using Bazănt’s analysis as a rationale, the NIST report limits its own investigation to the events leading up to the “initiation” of collapse, claiming that everything thereafter was inevitable and required no further investigation. NIST thereby sidesteps any consideration of what actually happened during the collapse itself, including evidence that might bring the correctness of Bazănt’s analysis into doubt.

The Accelerating Destruction

The roofline of the North Tower appears to drop suddenly in what some observers loosely describe as “free fall” or “near free fall.” To measure the actual motion of the roof line, a high quality copy of a video by Etienne Sauret (similar to a version available on YouTube[8]) was used. The Sauret video shows the North Tower’s north face, which is identifiable by the presence of the aircraft impact hole. It is a particularly good video for our purposes because it shows a nearly level, nearly perpendicular view of the face of the tower taken from a distant stationary camera. A number of software packages allow the placement of markers frame-by-frame on a video clip for kinematic analysis. One such program is Tracker,[9] which is part of the Open Source Physics project.[10] The frame rate of the Sauret video clip, which is the standard NTSC rate of 30,000 frames per 1001 s, or approximately 29.97 fps, serves as the time base. The vertical scale was calibrated by the floor spacings which, apart from the sky lobby and the mechanical floors, are known to be 12 ft 0 in apart.[11] The vertical position of the roof line was marked every six frames (0.2 s intervals) and the data was exported to a spreadsheet for analysis. (See Table 1.)

Frame #	T (sec)	y (m)	vy (m/s)
216	0.00	82.397
222	0.20	82.399	0.010
228	0.40	82.401	0.010
234	0.60	82.403	-0.562
240	0.80	82.176	-1.708
246	1.00	81.720	-2.665
252	1.20	81.110	-3.400
258	1.40	80.360	-4.520
264	1.60	79.302	-5.860
270	1.80	78.016	-7.165
276	2.00	76.436	-8.485
282	2.20	74.622	-10.005
288	2.40	72.434	-11.505
294	2.60	70.020	-12.648

300	2.80	67.375	-13.968
306	3.00	64.433	-15.285
312	3.20	61.261	-16.240
318	3.40	57.937	-17.358
324	3.60	54.318	-18.300
330	3.80	50.617	-19.443
336	4.00	46.541

Table 1: Video Measurement Data–Frame numbers indicate every 6th frame relative to the start of the video clip. The frame rate of the video is NTSC standard, 29.97 fps, yielding a measurement interval of 0.20 s. The y-values are the height of the roof line relative to an arbitrary origin. Velocities are computed by the symmetric difference differentiation algorithm.

A graph of the height of the roof line vs. time (Figure 1) displays the characteristic shape of a parabola indicating a downward acceleration.

The vertical component of velocity was computed using a symmetric difference numerical differentiation algorithm,

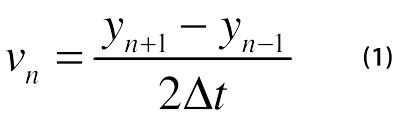
A graph of velocity vs. time (Figure 2) shows near uniformity of the downward acceleration from the 6th computed velocity point onward. When the roof line begins to fall, it quickly transitions to nearly uniform downward acceleration.

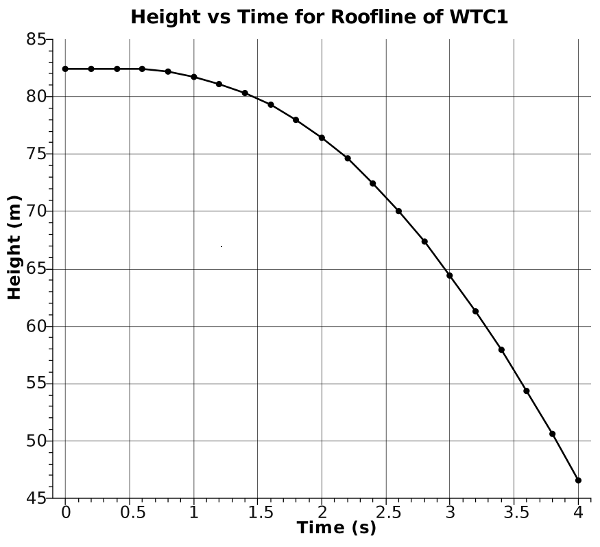
Figure 1: Graph of the height of the roof line (measured from an arbitrary origin) vs. time at 0.2 second intervals. Note that once it begins to fall the path appears approximately parabolic.

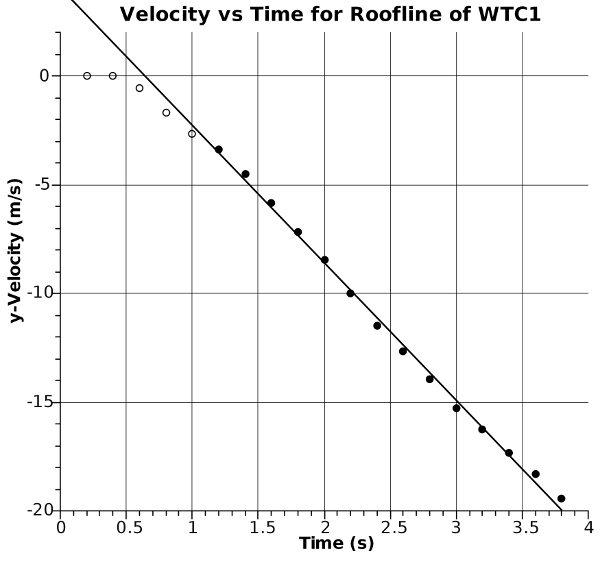
Figure 2: Velocity is here plotted as a function of time for the roof line of WTC1. The regression line is computed for the 6th computed velocity onward. The slope, in this context, is the acceleration: -6.31 m/s2 with an R2 value of 0.997.

Observations

For the current analysis we follow Bazănt’s simplifying assumptions [4, 5, 6, 7] by treating the upper section of the building as a solid block with mass m. The only two relevant forces acting on the falling block are gravity (mg) and an upward normal force (N) due to its interaction with the lower section of the building. Applying Newton’s Second Law and solving for N, we get

vmg − N = ma (2)

so

N = mg −ma (3)

Our data shows that from the sixth computed velocity data point onward, the upper block is accelerating uniformly (with an R2 value of 0.997) at a = -6.31 m/s2, or in other words, 64% of the acceleration of gravity. For this value of a,

N = mg − 0.64mg = 0.36mg (4)

Therefore the upward-acting normal force is 36% of the weight of the upper block, as illustrated in Figure 3.

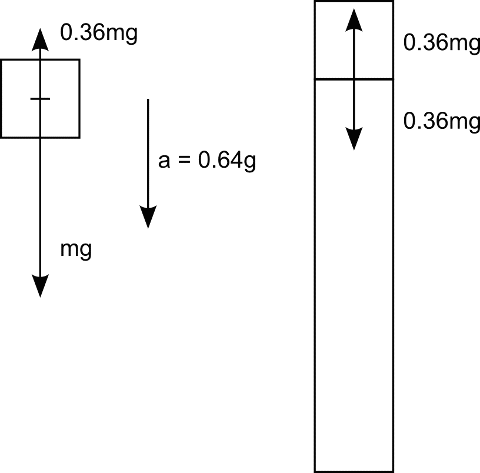
Figure 3: Consider the upper section of the building to be a block of weight mg. Since the acceleration of the block is measured to be downward at 0.64g, the net force acting on it must be 0.64mg. The gravitational force is mg, so the upward normal force must be 0.36mg. The upper and lower sections of the building exert equal but opposite forces on each other, so the load on the lower section of the building is 36% of the weight of the upper block.

Explicitly invoking Newton’s Third Law puts this result in another light. Since the forces in the interaction are equal and opposite, the falling block exerts a force of only 36% of its weight on the lower section of the building. In other words, as long as the falling block is accelerating downward we have the counter-intuitive result that the force it exerts on the lower section of the building is significantly less than its static weight. It is difficult to imagine how an upper block exerting a force of only 36% of its static weight could crush the larger, stronger, undamaged lower section of the building to the ground, when the building, at any level, was designed to support several times the weight above it. Assuming a safety factor of between 3 and 5 [12], the observed acceleration implies that close to 90% of the strength of the lower section of the building must have been eliminated by forces other than the supposed “pile driver,” suggesting that some sort of controlled demolition was at work.

One might argue, in terms of the strength of the various elements, that the impact of the falling block might crush the lower section of the building (although this assertion has been challenged [13]), but it cannot crush the lower block while it maintains its downward acceleration. Prof. Graeme MacQueen and Tony Szamboti have made a parallel observation, based on a similar measurement, in their paper, “The Missing Jolt: A Simple Refutation of the NIST–Bazănt Collapse Hypothesis.”[14] They point out that any increased force on the lower section of the building must be accompanied by a decrease in the momentum of the falling block. The transfer of momentum (which implies a loss of momentum for the upper block) is what gives rise to the impulse. The falling block can lose momentum only to the extent that it decelerates. It should therefore experience a “jolt” which we should be able to see in the video analysis. But from the fact that the upper block continues to move downward without deceleration, it is clear that there was no jolt despite the significant deformation of the building in the first three seconds.

The fact that a downward accelerating block would exert a force less than its own weight on the target block may be difficult to accept intuitively, but that is because our experience suggests the target block would resist the crushing blow. A rapidly moving hammer head driving a nail into a solid block of wood typically exerts a force on the nail many times the weight of the hammer head. But that is true only if the nail resists the blow. The large force that drives the nail into the wood is matched by a force that simultaneously decelerates the hammer head, which is why multiple blows are typically required. If, however, the nail is placed on a block of Styrofoam it will not significantly resist the blow. It will be driven into the block with very little force. The falling hammer head will meet so little resistance that it will be able to accelerate the whole time. In the case of WTC1, the falling block acts like the hammer head driving the nail into Styrofoam, but, changing the picture a little, it is the interface between the two blocks that is “soft.” Something other than the falling block (explosives?) must be destroying the structural integrity of the interface zone so that it offers only a small fraction of the resistance it was designed to provide.

Some might object to oversimplifying the model quite this much. It has been argued that the crushed material at the interface of destruction is accreted to the upper section so the mass of the falling block grows as it falls, producing an avalanche effect.[15] I would argue, from the fact that a major fraction of the mass landed outside the footprint of the building, that accretion was at most partial, but let us consider the effect of any such accretion. Newton’s Second Law applied to a system of variable mass can be stated

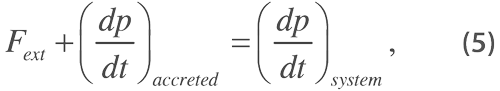
where p is momentum and Fext represents the net external force acting on the system. The accreted mass is initially at rest, so it brings no new momentum into the system:

Since p = mv we can write,

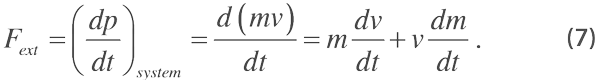
In our situation (letting the downward direction be positive),

F_ext = mg − N (8)

where N is the normal force, as in our earlier analysis. Recognizing

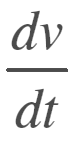
as simply the acceleration, a, we can write

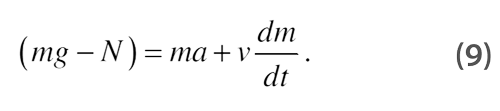
Solving for N, we have

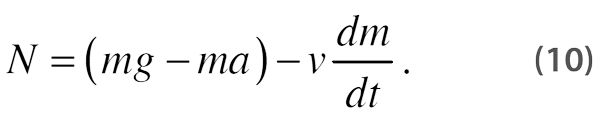
Note that this is the same as our previous result (Eq. [3]) except the normal force is reduced even further, since both v and

are positive.

Therefore, perhaps counter-intuitively, any accreted material reduces the effectiveness of an assumed pile driver. This result may become reasonably intuitive once one recognizes that the falling block must transfer some of its momentum to the accreted mass to bring it up to speed.

Summary

The fact that the roof line of the upper section of the North Tower continued to accelerate downward through the collision with the lower section of the building indicates that the upper section could not have been acting as a pile driver. As long as the roof line was accelerating downward, the upper block, exerted a force less than its own static weight on the lower section of the building. Any accretion of material into the upper block would have acted as an inertial brake, reducing the force of interaction even further. The undamaged lower section of the building was built to support several times the weight of the material above it, but whether or not we take the safety factor into account, the reduced force exerted by the falling mass could not have been what caused the violent destruction of the building seen in numerous videos. The persistent acceleration of the top section of the building is strong confirmation that some other source of energy was used to remove the structure below it, allowing the upper block to fall with little resistance.

Having assumed the existence of an indestructible falling block, with or without accretion, we have demonstrated that, given the observed acceleration, such a block could not possibly have destroyed the lower section of the building. When we turn to the video evidence we see that even the hypothesized existence of a persistent upper block is a fiction. Videos show that the section of the building above the plane impact point was the first section to disintegrate. It was significantly reduced in size prior to the onset of destruction of the lower section of the building. Once the roof line descends into the debris cloud there is no further evidence even of its continued existence. Whether or not it was completely destroyed early in the collapse is a moot point. We have shown that even if it continued to exist intact, it could not have played a significant role in the destruction of the building. A small section of a structure, consisting of a few floors, cannot one-way crush-down a significantly larger lower section of same structure by gravity alone.

Acknowledgments

I would like to express appreciation to the volunteer staff of Architects & Engineers for 9/11 Truth and others in the broader 9/11 Truth community who provided encouragement and critical discussion for this paper. Also I appreciate the correspondence with Charles M. Beck, who led me to think through the implications of accretion for this analysis.

References

1. T. W. Eagar and C. Musso, “Why did the World Trade Center collapse? science, engineering, and speculation,” JOM, vol. 53, no. 12, pp. 8-11, 2001. [Online]. Available: http://www.tms.org/pubs/journals/JOM/0112/Eagar/Eagar-0112.html [Accessed Mar 1, 2009]
2. (2006) NIST’s investigation of the Sept. 11 World Trade Center disaster—Frequently Asked Questions. [Online]. Available: http://wtc.nist.gov/pubs/factsheets/faqs_8_2006.htm [Accessed Mar 1, 2009]
3. NIST NCSTAR 1. [Online]. Available: http://wtc.nist.gov/NCSTAR1/PDF/NCSTAR%201.pdf [Accessed Mar 1, 2009]
4. Z. P. Bazănt, “Why did the World Trade Center collapse?” SIAM News, vol. 34, no. 8, pp. 2-6, 2001, (It is noteworthy that this paper was submitted on Sept. 13, 2 days after 9/11). [Online]. Available: http://www-math.mit.edu/~bazant/WTC/ [Accessed Mar 1, 2009]
5. Z. P. Bazănt and Y. Zhou, “Why did the World Trade Center collapse—Simple analysis,” J. Eng. Mech., vol. 128, no. 1, pp. 2-6, 2002.[Online]. Available: http://www-math.mit.edu/~bazant/WTC/WTC-asce.pdf [Accessed Mar1, 2009]
6. Z. P. Bazănt and M. Verdure, “Mechanics of progressive collapse: Learning from World Trade Center and building demolitions,” J. Eng. Mech., vol. 133, no. 3, pp. 308-319, 2007. [Online]. Available: http://www.civil.northwestern.edu/people/bazant/PDFs/Papers/466.pdf [Accessed Mar 1, 2009]
7. Z. P. Bazănt, Le, Greening and Benson, Journal of Engineering Mechanics, ASCE, Vol. 134 (2008), “What Did and Did not Cause Collapse of WTC Twin Towers in New York” Available: http://wtc7lies.googlepages.com/Bazant_WTC_Collapse_What_Did__Did_No.pdf
8. E. Sauret. 9/11: North Tower collapse (Sauret). [Online]. Available: http://www.youtube.com/watch?v=xGAofwkAOlo [Accessed Mar 1,2009]
9. D. Brown. Tracker ver 2.53. [Online]. Available: http://www.cabrillo.edu/~dbrown/tracker/ [Accessed Mar 1, 2009]
10. Open Source Physics project, NSF DUE-0442581. [Online]. Available: http://www.compadre.org/osp/ [Accessed Mar 1, 2009]
11. NIST NCSTAR 1, Figure 2-2. [Online]. Available: http://wtc.nist.gov/NCSTAR1/PDF/NCSTAR%201.pdf [Accessed Mar8, 2009]
12. T. Szamboti. (2007, May) The sustainability of the controlled demolition hypothesis for the destruction of the Twin Towers. [Online]. Available: http://www.journalof911studies.com/ [Accessed Mar 1, 2009]
13. G. Ross. (2006, Jun.) Momentum transfer analysis of the collapse of the upper storeys of WTC 1. [Online]. Available: http://www.journalof911studies.com/articles/Journal_5_PTransferRoss.pdf [Accessed Mar 1, 2009] Journal of 9/11 Studies – Feb 2010 17
14. G. MacQueen and T. Szamboti. (2009, Jan.) The missing jolt: A simple refutation of the NIST Bazănt collapse hypothesis. [Online]. Available: http://www.journalof911studies.com/volume/2008/TheMissingJolt7.pdf [Accessed Mar 1, 2009]
15. C. M. Beck. (2007, Nov.) Mathematical models of progressive collapse and the question of how did the World Trade Centers perish. [Online]. Available: http://arxiv.org/PS_cache/physics/pdf/0609/0609105v8.pdf [Accessed Mar 1, 2009]